1 Systemjordning / nollpunktsutrustning i dpPower Analyzer

 

2 Reaktor- och resistor-data

 

 

2.1 Reaktordata

 

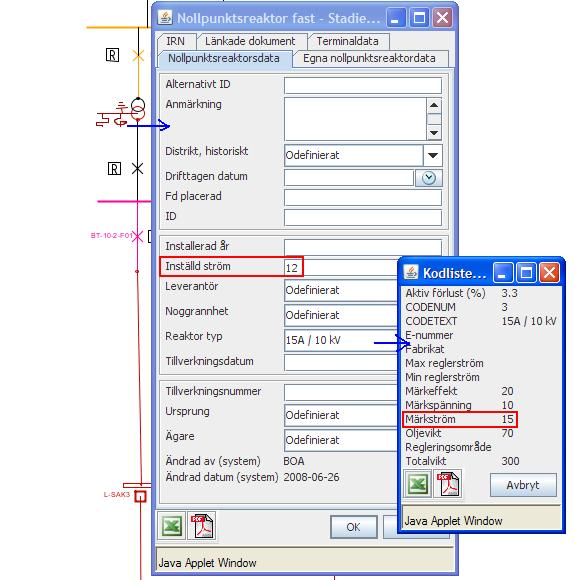
Om Inställd ström finns angiven på reaktorn kommer den att väljas före den angivna strömmen i kodlistan. (12A inte 15A väljes).

Aktiva förluster beräknas utifrån angiven aktiv förlust  i % (av inställd ström). Resultatet presenteras i rapport  HSP jordfelsrapport som strömbidrag uppifrån samt nedifrån, Sum resistiv str u A  Sum resistiv str n A

Bilaga: Aktiva reaktorförluster  

 

 

2.2 Resistordata

 

 

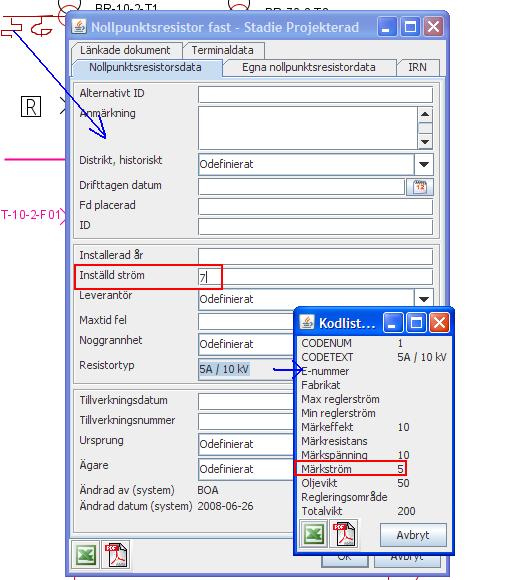
Om Inställd ström finns angiven på resistorn kommer den att väljas före den angivna strömmen i kodlistan. (7A inte 5A väljes).

 

 

3. Central kompensering

 

Nollpunkt definieras i fördelningsstationen samt bestyckas med nollpunktsreaktor / nollpunktsresistor.

3.1 Resistans/reaktansjordad nollpunkt i Y eller Z-kopplad transformatorlindning.

Konstruktion / tolkning.

 

Nollpunkten definieras med objekt Nollpunkt som länkas till lindning med rätt kopplingsart.

I nollpunkten finns möjlighet att lägga in ett ”övrigt” kapacitivt bidrag, en korrigeringsterm då man vet att det finns mera kapacitans i nätet än vad som erhålles från ledningsnätet. Det kan även läggas in ”avvikande” resistans för beräkning av högomigt jordfel (Default=3000 ohm).

 

 

Nollpunktsystemet kan byggas upp med ett antal objekttyper såsom:

Jordningskopplare  (Jordningsfrånskiljare)

Nollpunktsskena som är det objekt som reaktorer och motstånd skall kopplas mot.

Jordkablar, jordlinor.

Reaktor

Resistor

 

Detta bör räcka till för att definiera de flesta typer av jordningssytem i en Y eller Z-kopplad lindning.

De data som jordfelsberäkningen använder sig av är enbart data från nollpunkt och reaktor/resistor. Övriga objekt finns enbart för att kunna modellera olika systemkonstruktioner rent topologiskt såsom alternativa inkopplingsmöjligheter med hjälp av frånskiljarstatus.

 

Notera! att jordningskopplarna mellan resistor/reaktor och nollpunktsskena kan dokumenteras, men är ej nödvändigt.

 

Typisk nollpunkt för en transformator med Y eller Z-lindning.

 

3.2 Konstruerad nollpunkt vid D-kopplad krafttransformatorlindning

 

Om systemjordningen är en konstruerad nollpunkt vid t.ex D-kopplad på 10kV sidan kan detta åstadkommas genom att lägga in en ”nollpunktsbildare” (Jordningstransformator i menyer) mot samma 10kV skena som transformatorn är kopplad mot. I övrigt konstrueras nollpunkten p.s.s. som ovan.

 

 

 

3.3 Alternativt sätt att dokumentera en konstruerad nollpunkt vid D-kopplad krafttransformatorlindning

 

Enbart ett exempel på modifierad grafisk layout, i övrigt samma innehåll som i 3.2

 

 

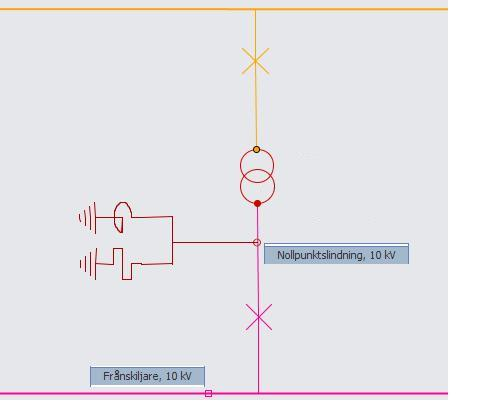
Nollpunktsbidare och jordningskopplare minskas i storlek men bibehålls hopkopplade, vilket gör att nätberäkningen kan koppla upp nollpunkten korrekt.

 

4. Lokal  kompensering

 

4.1 Lokal kompensering i nätstationstransformator

Två metoder finnes:

1.Samma princip som för den vanlig systemnollpunkten, komplett dokumentation.

2.Förenklad metod.

 

1. Komplett dokumentation med jordningskopplare mellan nollpunkt och nollpunktsskena.

Om uppsidans lindning i en nätstationstransformator är Y(N)-kopplad kan även lokal kompensation åstadkommes genom att lägga in en nollpunkt mot Y(N)-lindningen

 

 

 

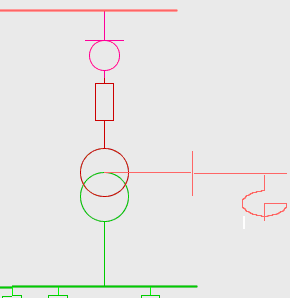
2 Förenklad metod

Placera enbart Nollpunkt samt Nollpunktsreaktor lokalkompensering.

Lokalkompenserings reaktorn kan kopplas direkt till nollpunkten.

 

 

 

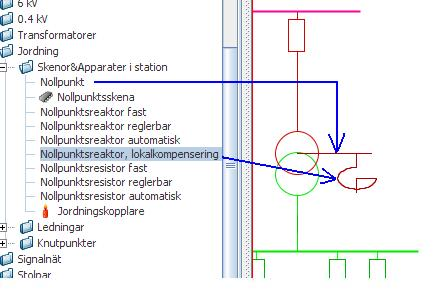
4.2 Lokal kompensering med lokal nollpunktsbildare

Lokal kompensering kopplad mot nollpunktsbildare (nollpunktslindning)

Om systemjordningen avser en lokal kompensering kan detta åstadkommas genom att lägga in en ”nollpunktslindning” kopplad till någon nätdel, exempelvis en skena. I övrigt konstrueras nollpunkten p.s.s. som ovan.

 

 

 

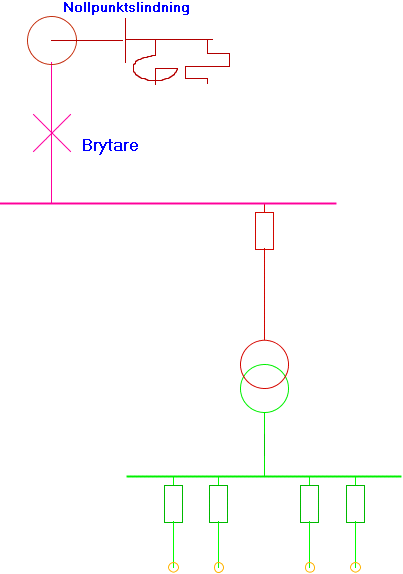
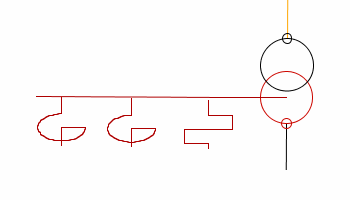
5. Parallella reaktorer

 

Det kan finnas parallella reaktorer i nollpunkten, inställd ström kommer att adderas för de parallella reaktorerna

 

6. Station med flera transformatorer och nollsystem.

 

 

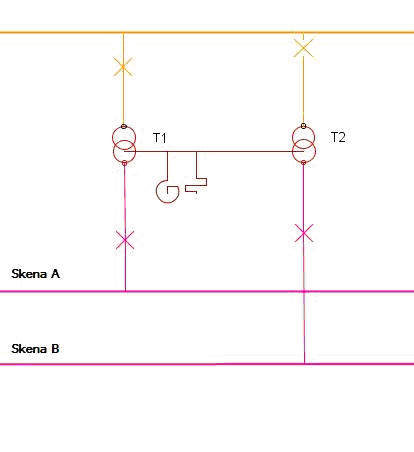
Om flera transformatorer finns i samma station med skilda nedsidor. Skena A har ej kontakt med Skena B i exemplet kan transformatorerna dela på samma nollpunkt eller ha 2 olika nollpunktssystem.

Resultat för respektive nollpunkt redovisas per transformator i HSP Jordfelsrapport.

 

 

 

 

 

7. Övrigt

Om nollpunktsutrustning saknas antas att ett MV-nät har isolerad nollpunkt samt att ett LV-nät är direktjordat.

 

Bilaga Reaktorförluster.

 

Aktiva reaktorförluster

 

Serierepresentation

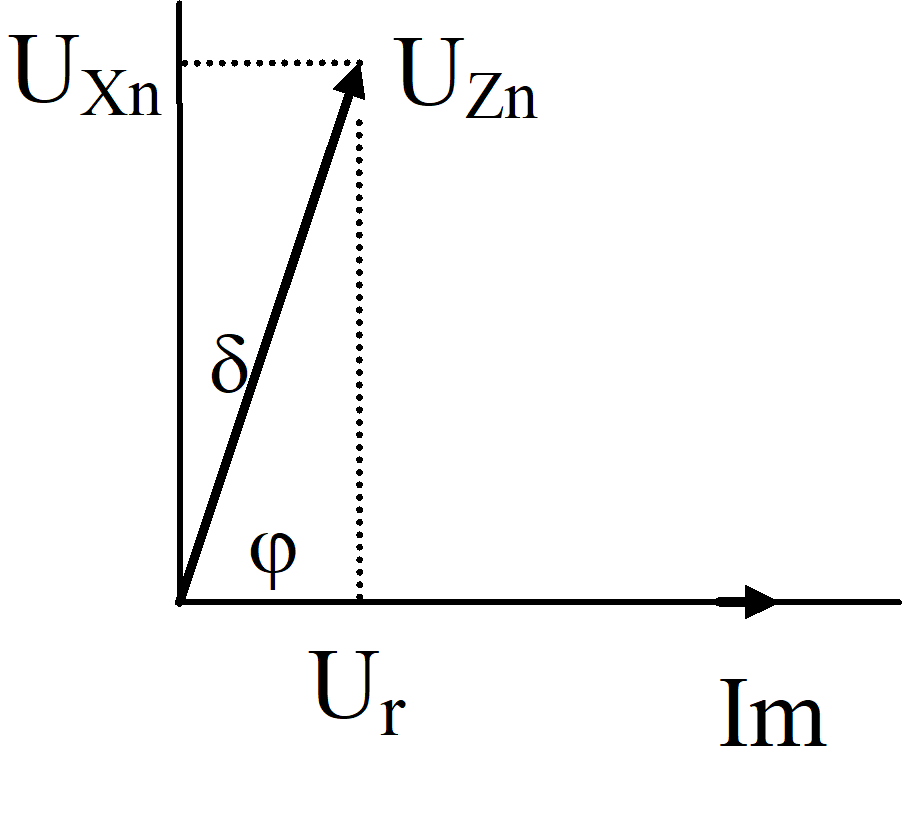
En reaktors (spoles) aktiva förluster kan representeras som en liten resistans r i serie med reaktansen Xn där

 

 r = p Xn                                                        (1)

 

 p   =  tand (= r/Xn) = reaktorns förlustfaktor (=r I2m/(Xn I2m)

 d = 90° - j = reaktorns förlustvinkel

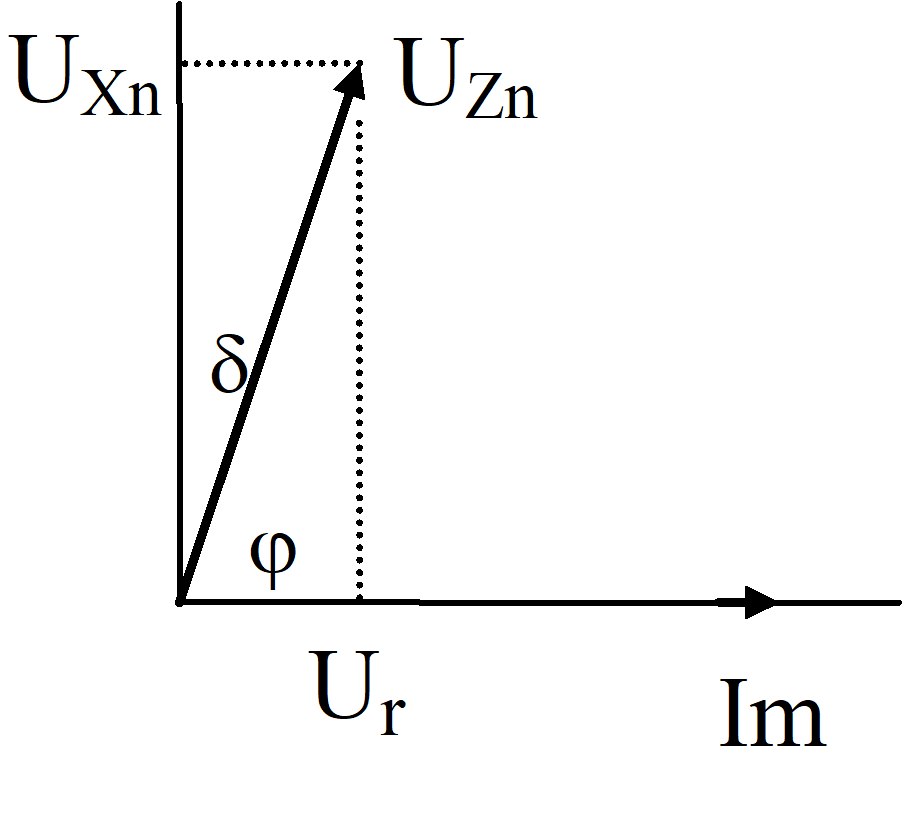
 │Zn│= Xn (1 + (r/Xn)2 )1/2 = Xn (1 + p2 )1/2 =  Um/Ö3/Im

 Um         är reaktorns märkspänning (huvudspänning) ; │UZn│= Um/Ö3

 Im är reaktorns märkström

 

 

 

                                                     

 

 

 

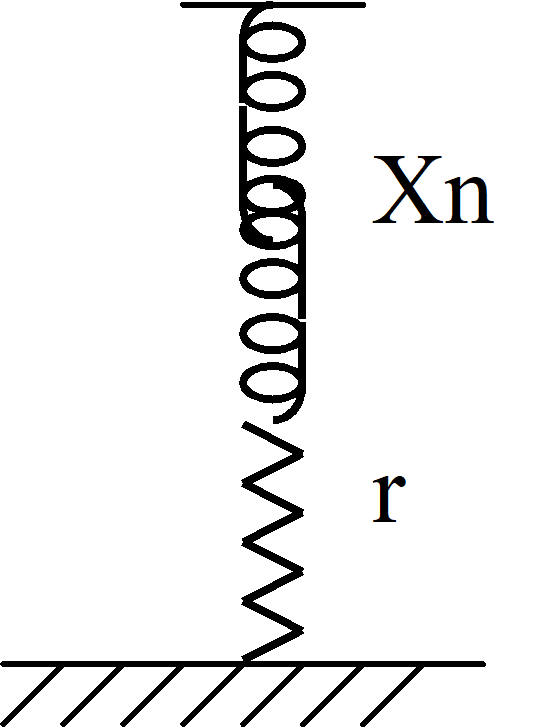
Det ger

 Zn = r + jXn

 

 Yn = 1/(r + jXn) = (p Xn - jXn)/(p2 X2n + X2n)

 

         = (p - j)/( p2+ 1)/Xn

 

Sätt ekvivalenta R’ och X’

                                                                             

 Yn = 1/R’ - j 1/X’

 

Identifiering ger

 

1/R’ = p/( p2+ 1)/Xn        ;  R’ = ( p2+ 1)/p Xn       (» Xn/p = X2n /r    om p << 1)            (2)

1/X’ = 1/( p2+ 1)/Xn        ;  X’ = ( p2+ 1) Xn            ( » Xn                        )

 

Lagras som nollpunktsdata  RSH( )= R’  ; XSH( ) = X’

 

 

Parallellrepresentation

 

Förlusterna kan också direkt representeras som

en stor resistans R parallell med reaktansen X

 

 Förlustfaktorn p = R IR2/(X IX2 )        

 

                                        = X/R        (3)                

 där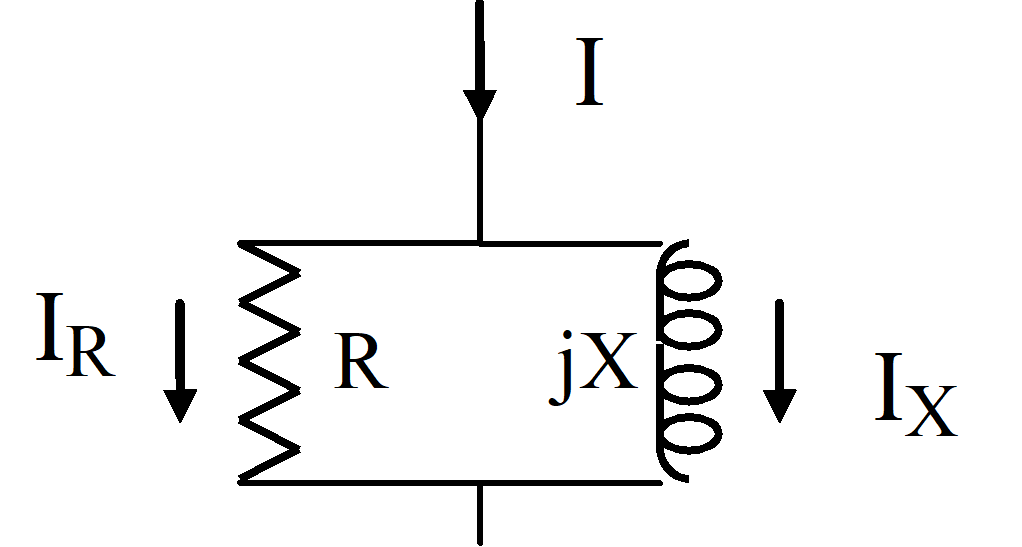                                                                          

 

 IR = jX/(R+jX) I     ; IX = R/(R+jX) I

 

 IR2 = IR I*R                    ; IX2 = IX I*X                ; IR2/IX2 = X2/R2 = p2 , dvs  p=│IR│/│IX│

 

Ur (1) och (3) erhålls

 

 p = r/Xn = X/R =│IR│/│IX│)        om p<<1 är        Xn = X                        (4)

 

                         R│IR│= X│IX│ = Um/Ö3

 

Omräkning av parallell- till seriekrets ger (omräkning av serie- till parallellkrets i (2))

 

Z = r + jX  º RjX/(R+jX) = (RX2 + j R2X)/(R2(1+X2/R2))

                                        = X2/R +jX                om p<< 1                        (5)

 

För parallellkretsen kan X erhållas ur märkdata enligt följande

 

 │IX │X =│R/(R+jX)│Im X = 1/(1+p2)1/2 Im X = Um/Ö3

 

 X/(1+p2)1/2 = Um/Ö3/Im

 

Sammanfattat visar sambanden (1) - (5) att , om p<< 1 , är en serierepresentation r av förlusterna ekvivalent med en parallellrepresentation R = X2/r  och en parallell-representation R är ekvivalent med en serierepresentation r = X2/R .

 

Oberoende av storleken på p kan man valfritt representera aktiva förlusterna via serie- eller parallellrepresentation. För stora p blir reaktanserna Xn och X olika men X’ och X blir lika även då, och därmed även R’ och R

 

X’ = (1+p2) Xn  =(1+p2)/(1+p2 )1/2 Um/Ö3/Im = (1+p2 )1/2 Um/Ö3/Im =  X  

 

 

Reaktiva effekten vid seriere QS - och parallell QP - representation

 

 QS = Xn I2m = Um/Ö3/(1+p2 )1/2  Im

 

 QP = X I2X = X R2/(R2+ X2) I2m = X I2m/(1+p2 ) = Um/Ö3/(1+p2 )1/2  Im