Aktiva reaktorförluster

 

 

Serierepresentation

En reaktors (spoles) aktiva förluster kan representeras som en liten resistans r i serie med reaktansen Xn där

 

 r = p Xn                                                        (1)

 

 p   =  tanδ (= r/Xn) = reaktorns förlustfaktor (=r I2m/(Xn I2m)

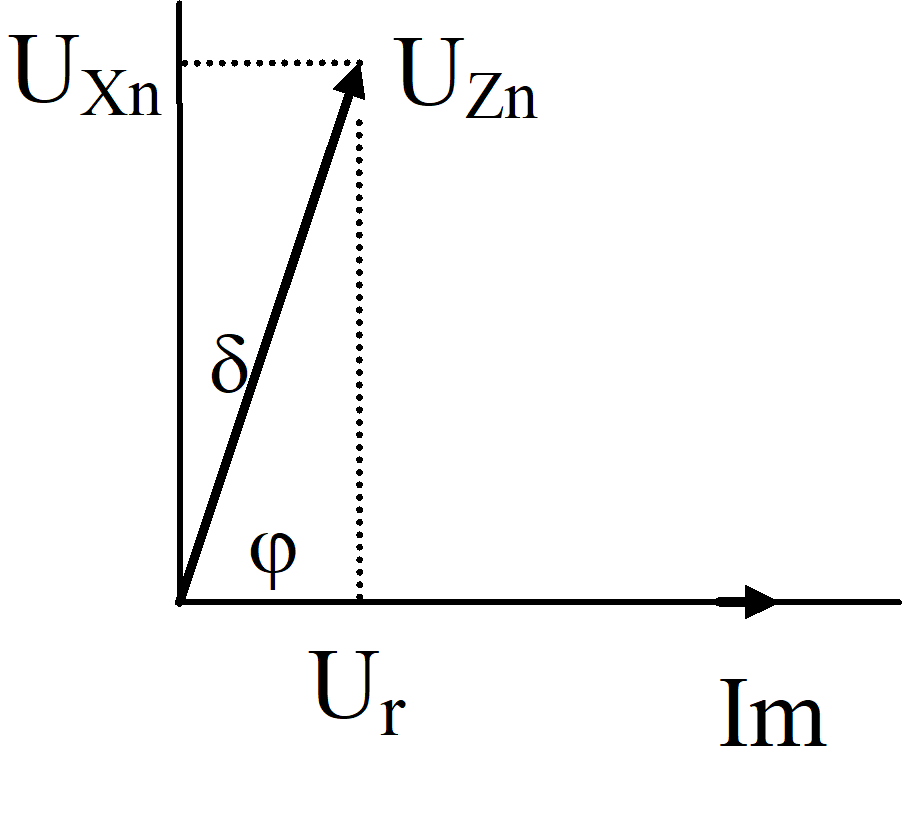
 δ = 90° - φ = reaktorns förlustvinkel

 │Zn│= Xn (1 + (r/Xn)2 )1/2 = Xn (1 + p2 )1/2 =  Um/√3/Im

 Um         är reaktorns märkspänning (huvudspänning) ; │UZn│= Um/√3

 Im är reaktorns märkström

 

 

 

                                                             

 

 

 

 

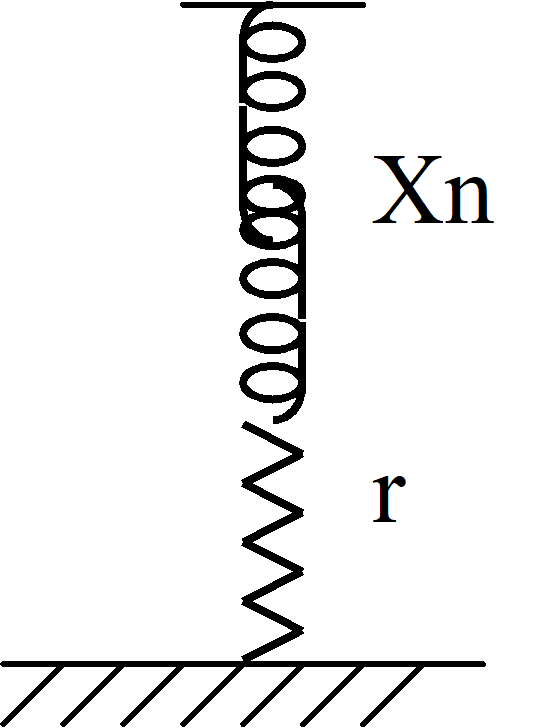
Det ger

 

 Zn = r + jXn

 

 Yn = 1/(r + jXn) = (p Xn - jXn)/(p2 X2n + X2n)

 

         = (p - j)/( p2+ 1)/Xn

 

Sätt ekvivalenta R’ och X’  

                                                                             

 Yn = 1/R’ - j 1/X’                                      

 

Identifiering ger

 

 1/R’ = p/( p2+ 1)/Xn        ;  R’ = ( p2+ 1)/p Xn       (≈ Xn/p = X2n /r    om p << 1)            (2)

 1/X’ = 1/( p2+ 1)/Xn        ;  X’ = ( p2+ 1) Xn            ( ≈ Xn                        )

 

Lagras som nollpunktsdata  RSH( )= R’  ; XSH( ) = X’

 

 

Parallellrepresentation

 

Förlusterna kan också direkt representeras som en stor resistans R parallell med reaktansen X

 

 Förlustfaktorn p = R IR2/(X IX2 )        

                                                                         

                                        = X/R        (3)                

 där

 

 IR = jX/(R+jX) I     ; IX = R/(R+jX) I

 

 IR2 = IR I*R                    ; IX2 = IX I*X                ; IR2/IX2 = X2/R2 = p2 , dvs  p=│IR│/│IX│

 

Ur (1) och (3) erhålls

 

 p = r/Xn = X/R =│IR│/│IX│)        om p<<1 är        Xn = X                        (4)

 

                         R│IR│= X│IX│ = Um/√3

 

Omräkning av parallell- till seriekrets ger (omräkning av serie- till parallellkrets i (2))

 

 Z = r + jX ≡ RjX/(R+jX) = (RX2 + j R2X)/(R2(1+X2/R2))

                                        = X2/R +jX                om p<< 1                        (5)

 

För parallellkretsen kan X erhållas ur märkdata enligt följande

 

 │IX │X =│R/(R+jX)│Im X = 1/(1+p2)1/2 Im X = Um/√3

 

 X/(1+p2)1/2 = Um/√3/Im

 

Sammanfattat visar sambanden (1) - (5) att , om p<< 1 , är en serierepresentation r av förlusterna ekvivalent med en parallellrepresentation R = X2/r och en parallell-representation R är ekvivalent med en serierepresentation r = X2/R .

 

Oberoende av storleken på p kan man valfritt representera aktiva förlusterna via serie- eller parallellrepresentation. För stora p blir reaktanserna Xn och X olika men X’ och X blir lika även då, och därmed även R’ och R

 

       X’ = (1+p2) Xn  =(1+p2)/(1+p2 )1/2 Um/√3/Im = (1+p2 )1/2 Um/√3/Im =  X  

 

 

Reaktiva effekten vid seriere QS - och parallell QP - representation

 

 QS = Xn I2m = Um/√3/(1+p2 )1/2  Im

 

 QP = X I2X = X R2/(R2+ X2) I2m = X I2m/(1+p2 ) = Um/√3/(1+p2 )1/2  Im