Series representation

The active losses in a reactor can be represented as a small resistance, r, in series with the reactance, Xn, where

 

r = p Xn                                (1)

 

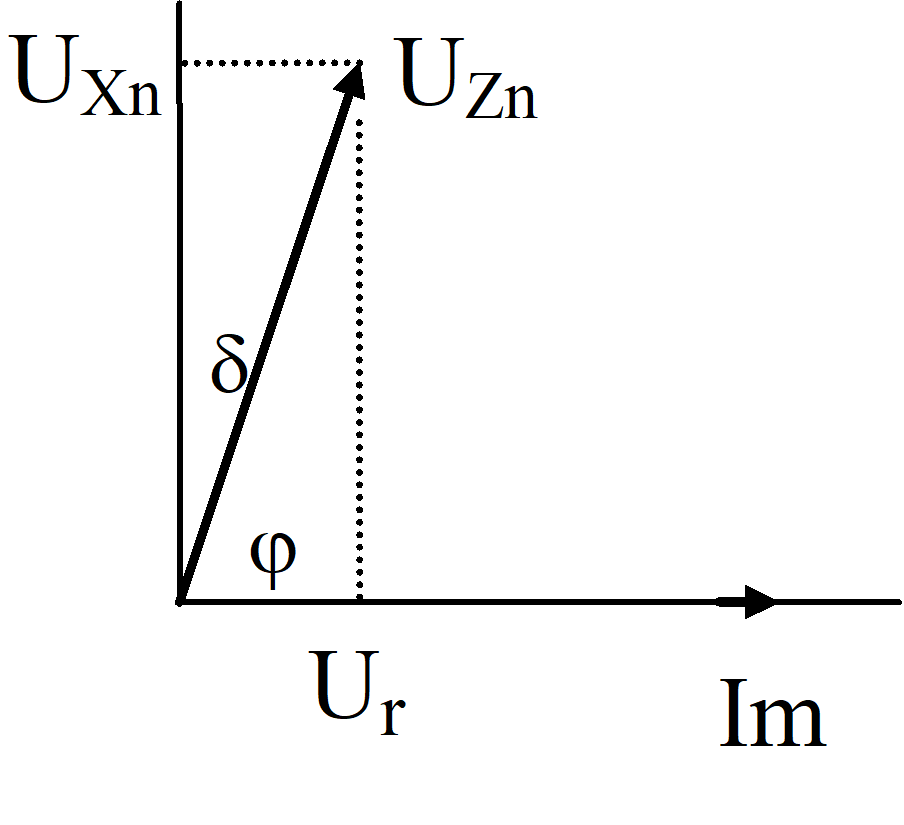
p = tan б (= r/Xn) = loss factor of the reactor (= r I²m / (Xn I²m)

б = 90° - φ = loss angle of the reactor

 

¦Zn¦= Xn (1 + (r / Xn)² )½ = Xn (1 + p²  ) ½= Um / √3 / Im

 

Um is the reactor rated voltage (phase-phase voltage) ;

UZn│= Um/√3

 

Im is the rated current of the reactor

 

                                                 

 

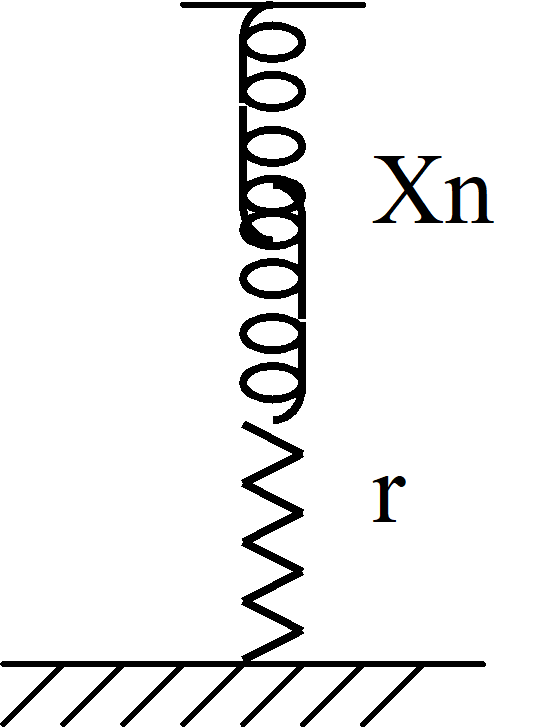
Which gives

 

Zn = r + jXn

 

Yn = 1 / (r + jXn) = (p Xn - jXn) / (p² X²n + X²n)

 

= (p - j) / ( p²+ 1) / Xn

 

Set equivalent R’ and X’

                                                                             

 

Yn = 1/R’ - j 1/X’

 

Identification gives…                                                                                                        (2)

 

1/R’ = p / ( p²+ 1) / Xn ; R’ = (p²+ 1) / p Xn (Xn / p = X²n / r if p << 1)

 

1/X’ = 1 / (p²+ 1) / Xn ; X’ = (p²+ 1) Xn     ( ≈ Xn)

 

Stored as neutral point data RSH( ) = R’ ; XSH( ) = X’

 

Parallel representation

The losses can also be directly represented as a large resistance R in parallel to the reactance X.

 

Loss factor p = R IR² / (X IX²)                                                                        

 

= X / R                                                         (3)

where…

 

IR = jX / (R + jX) I ; IX = R / (R + jX) I

 

IR² = IR I*R    ;    IX² = IX I*X    ;    IR²/IX² = X² / R² = p²,     i.e.    p = ¦IR¦/¦IX¦

 

From (1) and (3) can the following be obtained…

 

p = r / Xn = X / R = ¦IR¦ / ¦IX¦)                if p << 1 then Xn = X                    

 

R¦IR¦= X¦IX¦ = Um / √3                                 (4)

Re-calculation of parallel- to a serial circuit  gives (re-calculation of serial- to parallel circuit in (2))

 

Z = r + jX  ≡  RjX/(R+jX)  =  (RX² + j R²X) / (R² (1+X²/R²))

 

= X²/ R + jX                 if p << 1

 

For the parallel circuit can X be obtained from rated data according to…                        (5)

 

¦IX ¦X = ¦R / (R + jX) ¦ Im X = 1 / (1 + p²)½ Im X = Um / √3

 

X / (1 + p²)½ = Um / √3 / Im

 

To summarize, with references to (1) to (5) this shows that if p << 1, then a serial representation, r, of the losses is equivalent to a parallel representation R = X² / r and a parallel representation R is equivalent to a serial representation r = X² / R.

 

Independent of the size of p, it is possible to optionally represent the active losses via serial- or parallel presentation. For large p-values the reactance Xn and X will be different, but X’ and X will be the same and hence also R' and R.

 

X’ = (1 + p²) Xn = (1 + p²) / (1 + p² )½ Um / √3 / Im

= (1 + p² )½ Um / √3 / Im = X

 

The reactive power for serial QS- and parallel QP – representation

 

QS = Xn Im² = Um / √3 / (1 + p² )½ Im

 

QP = X I² X = X R²/ (R²+ X²) Im²

= X Im² / (1 + p²) = Um / √3 / (1 + p² )½Im