Fellägesbestämning
Fellägesbestämningen vid enfasigt jordfel sker iterativt i två steg, där de två stegen upprepas tills felimpedansen och felläget bestämts:
1. Beräkning av jordfelsimpedansen Zj med hjälp av en modell med approximativ nätrepresentation, beskriven i avsnitt 1.
2. Beräkning av jordfelsströmmarna med hjälp av en fullständig nätrepresentation, beskriven i avsnitt 2, med Zj från steg 1 insatt.
1. Modell med approximativ nätrepresentation
1.1 Approximativ serieimpedans Z’ för enfasigt jordfel
Z’k = 2 Z’+k + Z’0k (1.1)
där
Z’+k = resulterande plusföljds serieimpedans i knutpunkt k
Z’0k = Z0t + Z+Lk + 3 ZNk
= approximativ, resulterande nollföljds serieimpedans i knutpunkt k
Z0t = transformatorns nollföljdsimpedans
Z+Lk = plusföljds serieimpedans från transformatorn till knutpunkt k
| ZNk = nolledarens/skärmens impedans från transformatorns jordningspunkt till knutpunkt k |
Enfasiga jordfelsströmmen IR tecknas som
| IR = 3VR0k/( Z’k + 3 (Z’n + Zjk )) (1.2) |
| = VR0k/( Z’k/3 + Z’n + Zjk ) (1.3) |
där
| VR0k är spänningen i fas R i felstället k innan jordfelet inträffar |
| Zjk är jordfelsimpedansen i felstället k |
| Z’n är nollpunktsimpedansen Zn parallellt med nätets kapacitiva |
| nollföljds-reaktans till jord (1/(3jωC0) |
För representation av den approximativa serieimpedansen i ekvivalenten nedan införs beteckningen ZEJ för nätets serieimpedans plus jordfelsimpedansen, dvs
ZEJ = Z’k/3 + Zjk (1.4)
1.2 Beräkning av jordfelsströmmar med approximativ modell
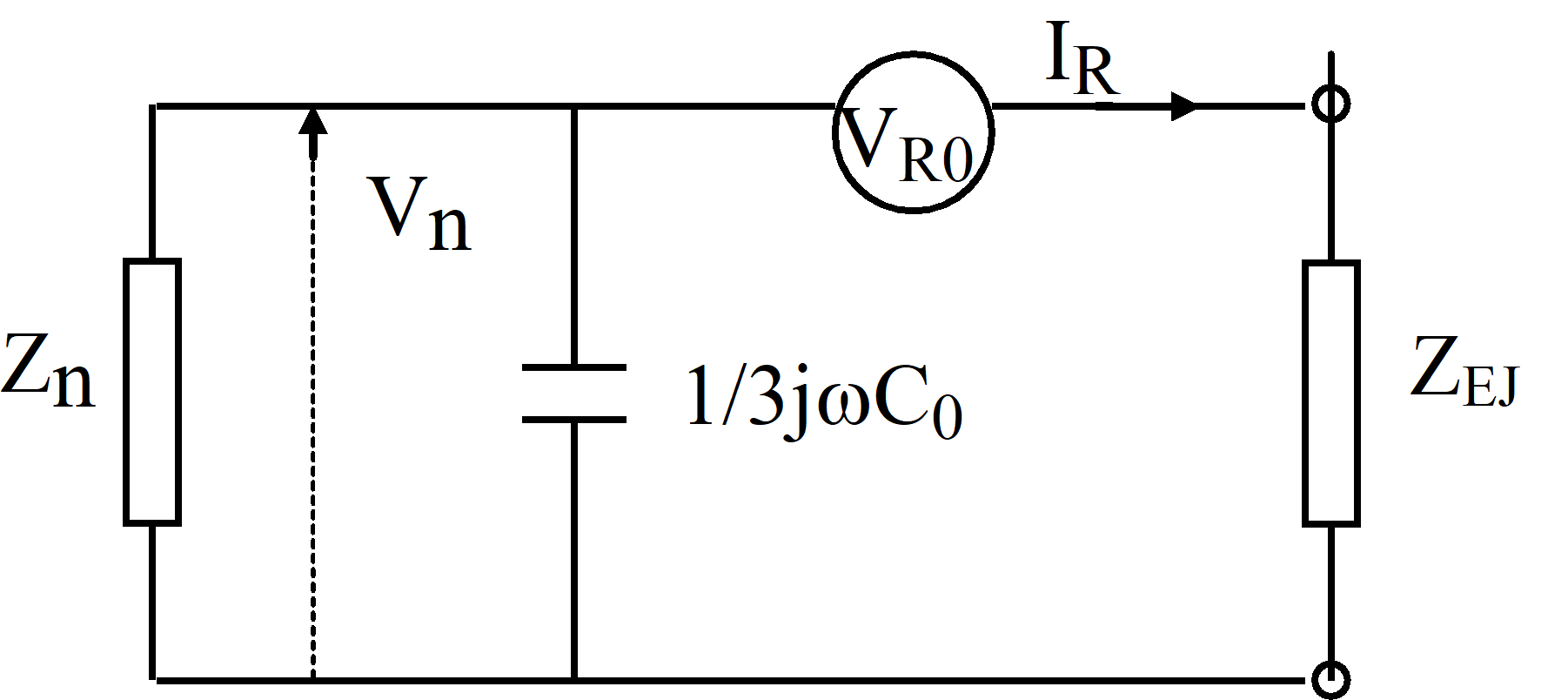
Fig. 1.1 Approximativ ekvivalent för enfasigt jordfel
Ur ekvivalenten erhålls
IR = VR0/(ZEJ + Z’n) (1.5)
där
1/ Z’n = 1/Rn + j(3ωC0 - 1/ωLn) (1.6)
Rn inkluderar även, förutom nollpunktsresistorer, resistanser som representerar nollpunktsreaktorers resistiva förluster, även utlokaliserade
Ln inkluderar även induktanser för utlokaliserade nollpunktsreaktorer
C0 inkluderar även uppmätt övrig kapacitiv ström, inklusive i utlokaliserade
nollpunkter, omräknad till kapacitanser vid nominell spänning
Nollpunkts- (nollföljds-) spänningen blir
Vn = - IR*Z’n = - VR0/( ZEJ /Z’n + 1) (1.7)
= - κ*VR0
där
κ = 1/( ZEJ /Z’n + 1) (1.8)
Vid försumbar jordslutningsimpedans ZEJ är faktorn k = 1.
Jordslutningsströmmen uppdelning per radial illustreras av Fig. 1.2
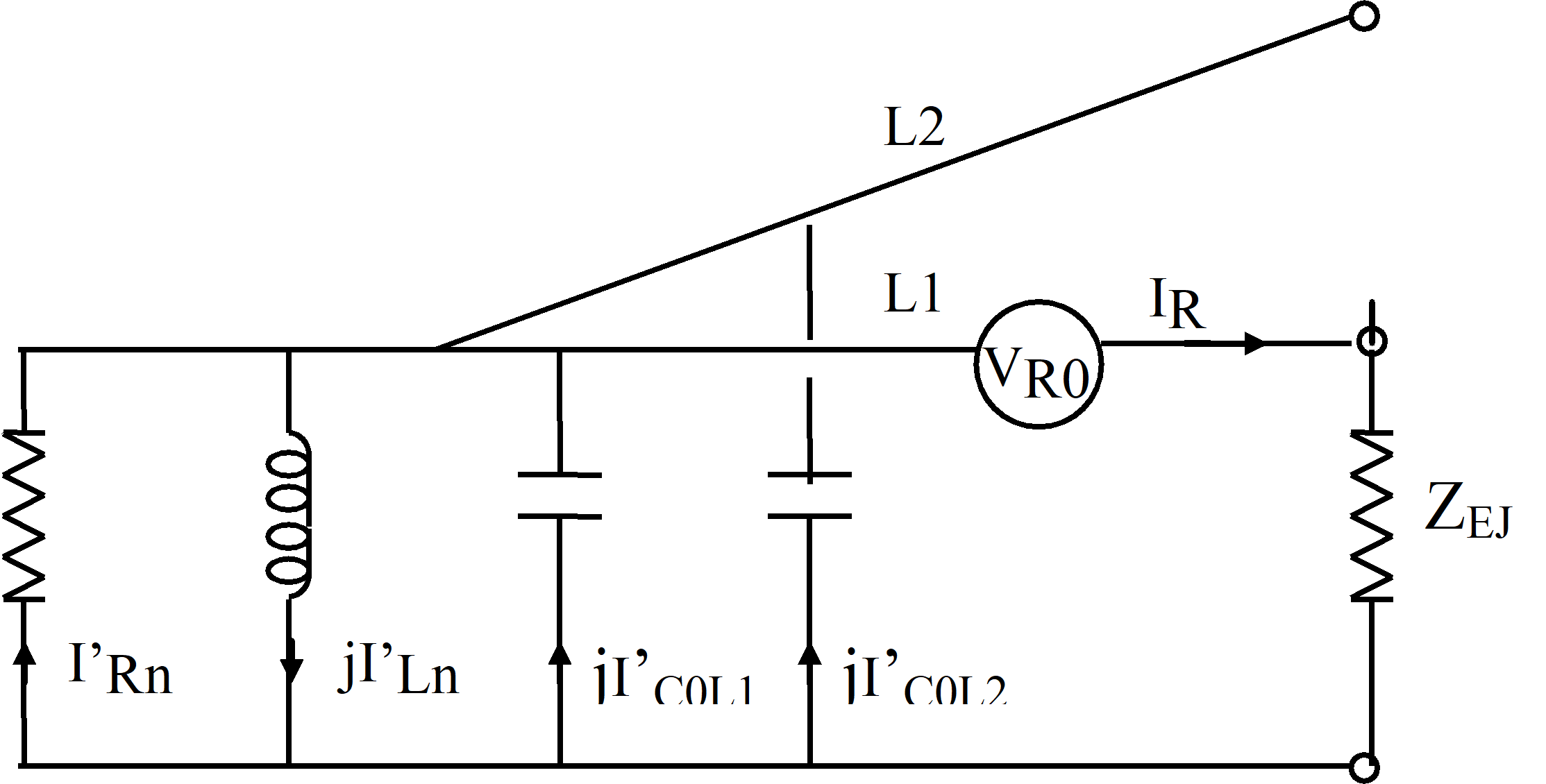
Fig. 1.2 Jordslutningsströmmens uppdelning per radial
Vid fel på radial L1 passeras ledningarnas skydd av strömmarna
L1) I’L1 = κ IL1 = κ (IRn- IRnL1 + j( IC0 - IC0L1 - ILn + ILnL1)) (1.9)
L2) I’L2 = κ IL2 = - κ ( IRnL2 + j(IC0L2 - ILnL2)) (1.10)
Där strömbidrag även kommer från utlokaliserade nollpunkter, inklusive aktiva reaktorförluster och uppmätt övrig kapacitiv ström.
2. Fullständig modell med nätkapacitanserna och utlokaliserade nollpunkter fördelade i nätets knutpunkter, med Y-matris representation av nätet
2.1 Nätrepresentation med faktoriserade Y-matriser (plus- och nollföljd)
I ett elektriskt kraftnät kan sambandet mellan strömmar och spänningar tecknas som
Y V = I (2.1)
där
I = vektor av knutpunktsströmmar
V = vektor av knutpunktsspänningar
Y = G + jB = nätets knutpunktsadmittansmatris
G = konduktans ; B = susceptans
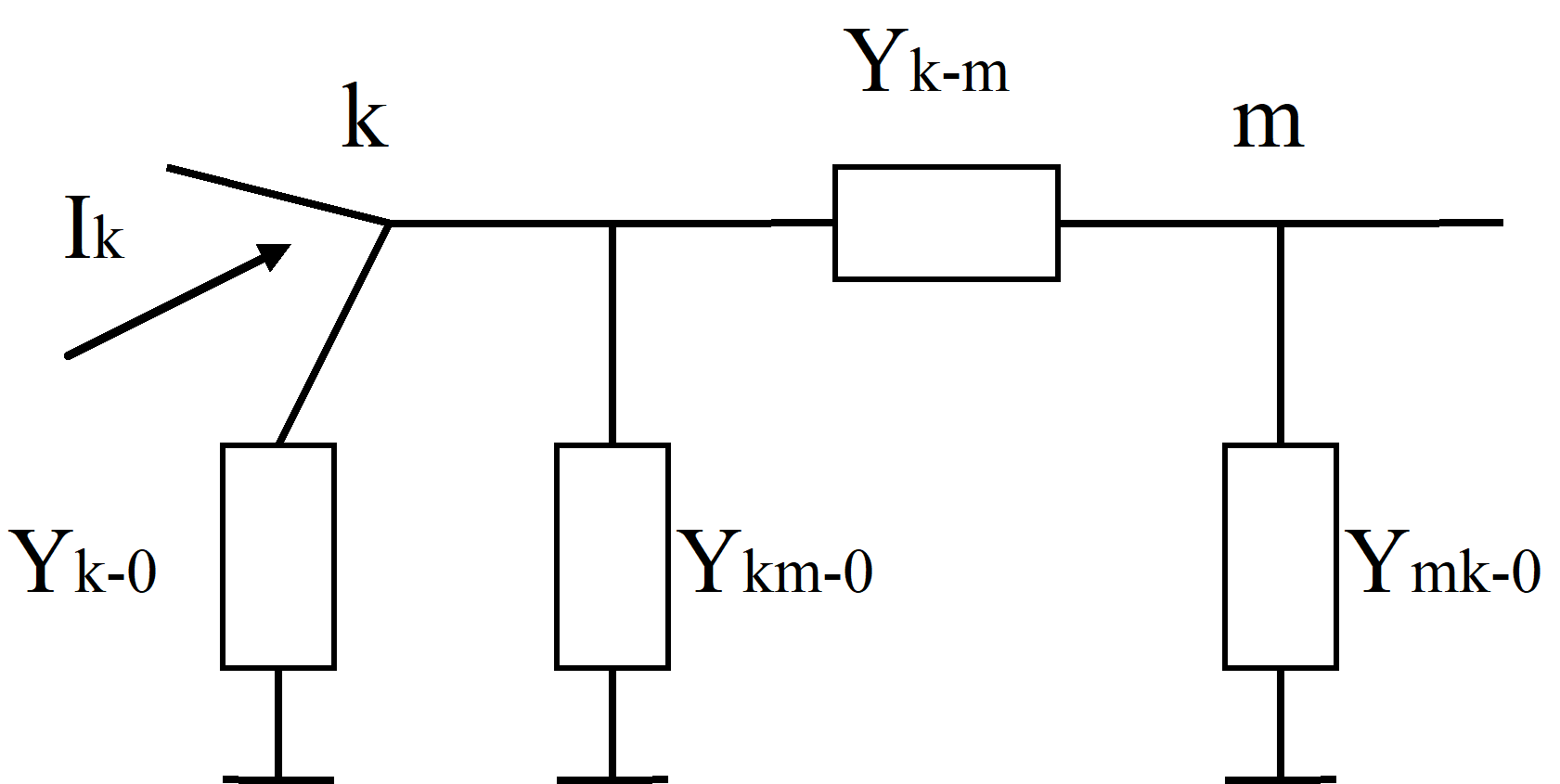
Fig. 2.1 Representation av elektriskt nät
Nätelementen representeras i form av pi-länkar enligt Fig. 2.1 där
Yk-m = pi-ekvivalent serieadmittans för sektion k-m
Ykm-0 = pi-ekvivalent shuntadmittans i knutpunkt k för sektion k-m
Ykm-0 = d:o i knutpunkt m
Yk-0 = admittans för shuntelement i knutpunkt k (kondensator, reaktor,
generator)
Injicerad knutpunktsström Ik tecknas som
Ik = Vk Yk-0 + Vk ΣmYkm-0 +Σm(Vk - Vm)Yk-m
= (Yk-0 + Σm(Ykm-0 +Yk-m))Vk - ΣmYk-m Vm (2.2)
där summeringen sker över alla knutpunkter m direkt anslutna till knutpunkt k.
Admittansmatrisens diagonalelement och icke-diagonalelement i (2.1) är enligt (2.2)
Ykk = Yk-0 + Σm(Ykm-0 +Yk-m)) (2.3)
Ykm = - Yk-m
Sambandet (2.1) kan även skrivas om som
V = Y-1 I
= Z I (2.4)
där
Z = R + jX = nätets knutpunktsimpedansmatris
R = resistans; X = reaktans
Vid simulering av fel i en given punkt i nätet beräknar man ur Y-matrisen den aktuella kolonnen i Z-matrisen. Den kan tecknas som
Z(k) = Y-1 E (k) (2.5)
där E (k) är kolonn k i enhetsmatrisen, dvs en vektor med en etta i position k och nollor i övrigt. Det kan också tolkas som att injicering av en en p.u. ström i en knutpunkt k i nätet ger knutpunktsspänningar som är identiska med motsvarande kolonn i Z-matrisen.
Vid beräkning av (2.5) tillämpas matrisfaktorisering, i detta fall LDU – faktorisering, av det linjära ekvationssystemet (2.1) som allmänt kan tecknas som
A x = b (2.6)
Faktorisering av A ger
LDU x = b (2.7)
U x = y (2.8)
LD y = b (2.9)
Där
- L och U är undre och övre triangulära matriser med ettor i diagonalerna
- D är en diagonal-matris
- hjälpvektorn y löses för det glesa högerledet b med s.k. ’fast forward’ (FF)
substitution och division med D , enligt sambandet (2.9)
- vektorn x löses med ’backward’ (B) eller, om endast en delmängd av x-elementen önskas, med ’fast backward’ (FB) substitution
Den ovan beskrivna Y-matris metodiken används vid beräkning av enfasigt jordfel när man önskar representera nätet som pi-länkar, där ledningskapacitanserna och utlokaliserade nollpunkter är representerade som shuntar i knutpunkterna (se Fig. 2.1).
Vid beräkning av jordfel i en knutpunkt k beräknas plus- och nollföljds - Z-matris- kolonnerna Z+(k) och Z0(k) för knutpunkten (plus- och minusföljds-impedanserna antas vara lika) varefter strömmarna i felstället beräknas som
I+k = I- k = I0k = V+k0 /( 2 Z+kk + Z0kk+ 3 Zjk ) (2.10)
Spänningarna i en knutpunkt m i nätet beräknas som
V+m = V+m0 - Z+km I+k (2.11)
V-m = - Z+km I-k (2.12)
V0m = - Z0km I0k (2.13)
Impedanserna Z+kk , Z+km och Z0kk , Z0km är element i respektive kolonnerna Z+(k) och Z0(k)
2.2 Fel ute på ledningssektion
När man önskar beräkna felströmmar för fel ute på en ledningssektion mellan knutpunkter, t. ex. som här vid fellägesbestämning, används en metodik enligt följande beskrivning.
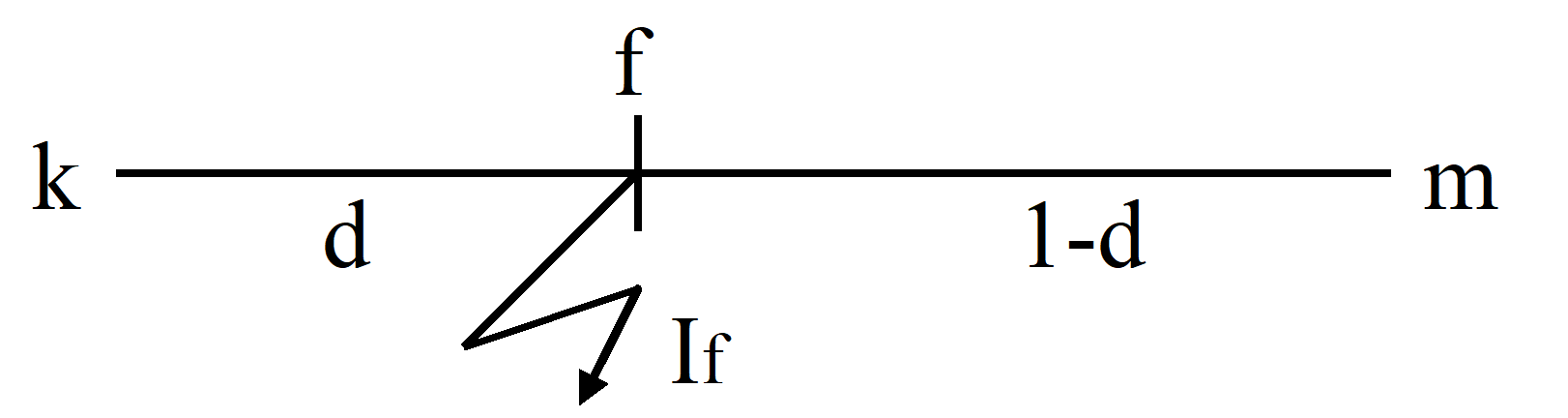
Fig. 2.2 Fel ute på ledningssektion
Fig. 2.2 ovan illustrerar fel i en punkt f ute på en ledningssektion k-m , på avståndet d från knutpunkt k. Följande samband mellan strömmar och spänningar kan ställas upp
Vf = Vk - d Zk-m Ik-f (2.14)
Vf = Vm - (1-d) Zk-m Im-f (2.15)
If = Ik-f + Im-f (2.16)
Sambanden (2.14) och (2.16) ger
Vf = Vk - d Zk-m If + d Zk-m Im-f (2.17)
Lösning av Im-f ur (2.15) och insättning i (2.17) ger
Vf = Vk - d Zk-m If + d Zk-m ((Vm -Vf)/((1-d) Zk-m))
= (1-d)Vk +dVm - d(1-d) Zk-m If (2.18)
Om 1 p.u. ström injiceras i en punkt ‘i’ blir spänningen i punkt f
Vif = Zfi = Vik - d Zk-m Iik-m
= Vik - d(Vik - Vim)
= (1-d)Zki + d Zmi i = 1, 2, ….. , n (2.19)
där övre index ‘i’ indikerar att kvantiteten härrör från 1 p.u. injiceringen i knutpunkt ‘i’ och n betecknar antalet knutpunkter i nätet.
Om 1 p.u. injiceras i punkt f erhålls enligt (2.18) sambandet
Vff = Zff =(1-d) Vfk + d Vfm + d(1-d) Zk-m
= (1-d) Zkf + d Zmf + d(1-d) Zk-m (2.20)
Insättning av (2.19) i (2.20) med i=k och i=m ger
Zff = (1-d)((1-d) Zkk + d Zmk + d((1-d) Zkm + d Zmm) + d(1-d) Zk-m
= (1-d)2 Zkk + 2d(1-d) Zkm + d2 Zmm + d(1-d) Zk-m (2.21)
Uttrycken (2.19) och (2.21) visar hur impedansmatriskolonnen för felstället f ute på ledningssektionen k-m erhålls med hjälp av impedansmatriskolonnerna för ändpunkterna och sektionens egenimpedans.
För ett rent radiellt nät utan shuntelement, t.ex. det approximativa nätet i avsnitt 1, är Zkm = Zkk och Zmm = Zkk + Zk-m. Insättning av dessa värden i (2.21) ger
Zff = Zkk + d Zk-m (2.22)
3. Algoritm för fellägesbestämning
3.1 Skattning av jordfelsimpedans
Värdet på parametern k beräknas ur de tre tidigare uppställda sambanden (1.7), (1.9) och (1.10)
κ = - Vn/VR0 (3.1)
κ = I’L1/IL1 (3.2)
κ = I’L2/IL2 (3.3)
där (3.1) avser nollpunkten, (3.2) avser felbehäftade radialen och (3.3) de friska radialerna.
Vn , I’L1 och I’L2 är uppmätta värden med okänd felimpedans och okänt felläge.
- VR0 , IL1 och IL2 är beräknade värden ur den approximativa modellen (ekvivalenten) med felimpedansen ZEJ = 0.
Enligt sambandet (1.8) är κ = 1/( ZEJ /Z’n + 1) vilket ger
ZEJ = Z’n (1-κ)/κ (3.4)
ZEJ beräknas ur vart och ett av sambanden /3.1) , (3.2) och (3.3) och ett medelvärde bildas.
Därefter beräknas Z’k ur den approximativa nätrepresentationen, enligt sambandet (1.1), varefter felimpedansen bildas ur uttrycket (1.4) som
Zjk = ZEJ - Z’k/3 (3.5)
och 3 Zjk sätts in i den fullständiga modellen i uttrycket (2.10) för enfasigt jordfel.
I första iterationen, innan något möjligt felläge bestämts, beräknas Z’k som ett medelvärde över nätets knutpunkter. I efterföljande iterationer tas felläget från den fullständiga modellen, dvs aktuell sektion k-m och position d, och sätts in i uttrycket (2.22) för radiellt nät.
3.2 Beräkning av felläge
Beräkning av felläge sker med den fullständiga modellen 2 och startar med att bestämma gränssektioner k-m i den felbehäftade radialen. En gränssektion definieras då som en sektion k-m sådan att:
-fel i knutpunkt k ger en felström I0fk som resulterar i en felström I0rk ut på radialen
som är lika med eller större än uppmätt ström I’r
-fel i knutpunkt m ger en felström I0fm som resulterar i en felström I0rm ut på
radialen som är mindre än uppmätt ström I’r
Strömmarna I0fk och I0fm beräknas ur sambandet (2.10) och strömmarna I0rk och I0rm ur beräknade nollföljdsspänningar, enligt sambandet (2.13), för mätsektionens knutpunkter rk och rm (m=rk och m=rm insatta i (2.13)) , och sektionens nollföljds - pi-länk.
Vid bestämning av felläget f på en sektion sker beräkningarna enligt principerna redovisade i avsnitt 2.2 där sambanden (2.19) och (2.21) används för beräkning av plusföljds- och nollföljds-impedansmatriskolonnerna för felpunkten f. Plus- och nollföljds-impedanserna Z+ff och Z0ff används för beräkning av felströmmen I0f . Nollföljds- impedanserna Z0f rk och Z0f rm och används för beräkning av nollföljdsspänningarna i mätsektionens knutpunkter rk och rm. Med dessa spänningar och sektionens nollföljds - pi-länk beräknas sedan felströmmen I0rf ut på radialen.
Avståndet d till felpunkten f bestäms genom intervallhalvering:
A1) sätt dmin = 0 och dmax = 1
A2) d = 0.5 (dmin + dmax ), om (dmax - dmin) )< eps1 har felläget identifierats
A3 beräkna felströmmen I0rf ut på radialen vid felläget d
| A4) om I0rf är lika med uppmätt ström I’r , eller (I’r -I0rf)< eps2 ), har felläget identifierats |
A5) om I0rf är större än uppmätt ström I’r sätts dmin = d, gå till A2
A6) om I0rf är mindre än uppmätt ström I’r sätts dmax = d, gå till A2
Vid beräkning av felläge enligt detta avsnitt 3.2 används strömmarnas absolutbelopp.
När felläget identifierats korrigeras jordfelsimpedansen Zjk = ZEJ - Z’k/3 ovan, (sambandet (3.5)) genom att approximativa serieimpedansen Z’k/3 omräknas via insättning av felläget i beräkningen av impedansen (2.22) för radiellt nät . Därefter startar en ny iteration med fellägesbestämning. När ändringen i jordfelsimpedansen från en iteration till en annan är mindre än ett givet gränsvärde avbryts iterationerna och felläget på denna gränssektion betraktas som bestämt.
Om den felbehäftade radialen har flera möjliga gränssektioner (möjliga felställen) startar den iterativa proceduren 3.2 på nytt.